卡特兰数

发表于 2021-11-28 更新于 2022-05-25 分类于笔记，算法

简介

卡特兰数是一个在组合数学里经常出现的一个数列，对卡特兰数来说，难以抽象出一个具体的意义预知对应，但它却是一个十分常见的数学规律，符合多种问题规律求解。从零开始，卡特兰数的前几项为1,1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845,35357670,129644790…

递推公式

基础公式:

\(C_{n+1}=C_0C_n+C_1C_{n-1}+...+C_{n-1}C_1+C_nC_0\\C_0=C_1=1\)

或者：

\[ C_{n+1}=\left\{ \begin{aligned} &\sum_{i=0}^nC_iC_{n-i},&n>1 \\ &1,&n=0,1 \end{aligned} \right\} \]

其中C表示Catalan数。

组合公式

\[ \begin{aligned} Catalan_n&=C_{2n}^n-C_{2n}^{n+1}\\ &=\frac{(2n)!}{n!∗n!}−\frac{(2n)!}{(n+1)!∗(n−1)!}\\ &=\frac1{n+1}(\frac{(2n)!∗(n+1)}{n!∗n!}−\frac{(2n)!}{n!∗(n−1)!})\\ &=\frac1{n+1}(\frac{(2n)!∗(n+1)}{n!∗n!}−\frac{(2n)!∗n}{n!∗n!})\\ &=\frac1{n+1}∗\frac{(2n)!∗(n+1)−(2n)!∗n}{n!∗n!}\\ &=\frac1{n+1}∗\frac{(2n)!}{n!∗n!}\\ &=\frac1{n+1}C_{2n}^n \end{aligned} \]

或者: \[ Catalan_n=\frac{4n+2}{n+2}Catalan_n \] 推导如下: \[ \begin{aligned} Catalan_{n+1}&=\frac1{n+2}C_{2n+2}^{n+1}\\ &\frac1{n+2}∗\frac{(2n+2)!}{(n+1)!∗(n+1)!}\\ &\frac1{n+2}∗\frac{(2n)!∗(2n+1)∗(2n+2)}{n!∗n!∗(n+1)^2}\\ &\frac1{n+2}∗\frac{(2n+1)∗(2n+2)}{(n+1)}∗\frac1{n+1}∗\frac{(2n)!}{n∗n!}\\ &\frac{2(2n+1)}{n+2}∗\frac1{n+1}∗C_{2n}^n\\ &\frac{4n+2}{n+2}Catalan_n \end{aligned} \]

其中的C代表组合数标记

应用

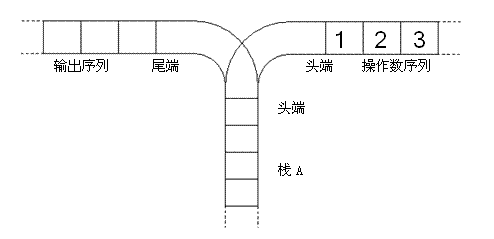
进出栈问题。将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）；将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作），使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，不同的输出序列数有多少种？
有2n个人排成一行进入剧场。入场费 5 元。其中只有n个人有一张 5 元钞票，另外n人只有 10 元钞票，剧院无其它钞票，问有多少中方法使得只要有 10 元的人买票，售票处就有 5 元的钞票找零？
一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果他从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？
对角线不相交的情况下，将一个凸多边形区域分成三角形区域的方法数？
n个结点可构造多少个不同的二叉树？

典型进出栈解法

序列1，2，3，4....n入栈在出栈，考虑n出栈时的位置，可将栈分为在其前面出栈和在其后面出栈两部分，以\(C_n\)代表序列长度为n时的不同输出序列的数量。若n为第一个出栈的数，其前面有\(C_0\)种输出方式，其后有\(C_{n-1}\)种输出方式，n第一个出栈的排列总数为\(C_0C_{n-1}\)；若考虑n第k个数出栈，在其前面出栈的数有\(C_{k-1}\)种出栈方式，在其后面出栈的数有\(C_{n-k+1}\)种出栈方式，此状态下的输出的总排列数量为\(C_{k-1}C_{n-k+1}\)；\(C_n\)为n在输出序列中不同位置时的所有不同排列数的加和：

\(C_{n+1}=C_0C_n+C_1C_{n-1}+...+C_{n-1}C_1+C_nC_0\)

通式解法

n=int(input())
catalan = [0]*(n+1)
if n<=1:
    print(1)
else:
    catalan[0]=1
    catalan[1] = 1
    for i in range(2,n+1):
        catalan[i] = sum([catalan[j]*catalan[i-j-1] for j in range(i)])

    print(catalan[n])

变形公式解法

n=int(input())
c = 1
for i in range(1,n+1):
    c *= (4*(i-1)+2)/(i+1)

print(int(c))