排序算法——快速排序

发表于 更新于 分类于 ， ， ，

介绍

快速排序（Quick Sort）是对冒泡排序的一种改进。它运用到了分治思想，对每一个子序列分别排序。其平均时间复杂度为\(O(nlog(n))\)，最坏时间复杂度为\(O(n^2)\)。虽然在时间复杂度上并没有显著的优势，但在实际运用中效率比同时间复杂度的一些算法要高。

实现

基本步骤

  • 选取一个基元素，作为排序的对比标准，一般选取数组的第一个元素，也可以在中间随机选取。
  • 选取左指针和右指针（数组的以一个元素索引和最后一个元素索引）。
  • 先从大往小移动右指针，当指针所指元素小于基元素时，将此元素覆盖到左指针处（此时左指针处的元素由基元素备份，此位置视为一个坑，可覆盖，同理覆盖后此时的右指针位置成为一个坑，可由接下来的元素填充），然后左指针右移一位。
  • 之后右指针不变从左往右遍历左指针，当左指针所指元素大于基元素时，将此元素填到右指针所指位置。
  • 重复上面两个步骤直到左右指针相等，将基元素填在指针相等的位置，此时所有大于基元素的数都在其右边，所有小于基元素的数都在其左边。至此完成了一个排序。
  • 对由基元素分割出来的两个数组再次按此步骤进行排序，一直递归下去，直至子数组的元素不需要排序（数组长度小于1）。

图解

将原数组中第一个元素作为基元素，同时设置左右指针。

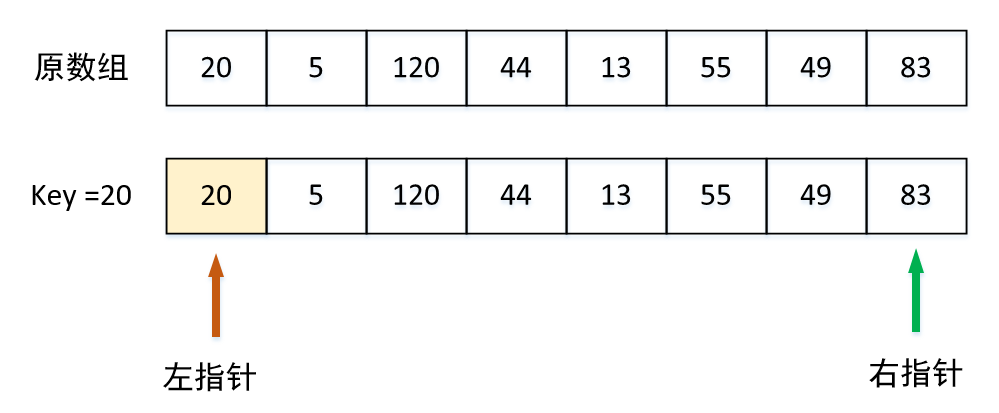
image-20210427224521335
image-20210427224521335

移动移动指针，直到找到小于基元素的数(13)，将其填入左指针位置，将左指针右移一位。

image-20210427225034407
image-20210427225034407

移动左指针，直到找到比基元素大的值(120)，将其覆盖到右指针位置，右指针左移一位。

image-20210427225339326
image-20210427225339326

轮到右指针的轮次，移动右指针找到比基元素小的，显然120和40都比基元素20大，当左右指针重合时(数组索引为2)，跳出循环，将基元素填入指针位置。

image-20210427225719310
image-20210427225719310

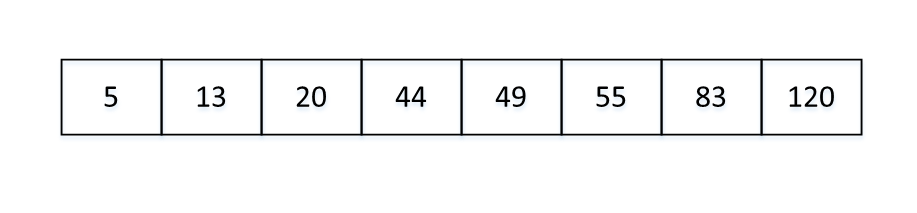
此时20的两边分别为小于其和大于其的数。对两个子数组，再次采用相同的方式来排序，直到所有元素排序完成。

image-20210427230155431
image-20210427230155431

最终排序完成数组为：

image-20210427230412301
image-20210427230412301

源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {20, 5, 120, 44, 13, 55, 49, 83};
        partial(arr, 0, arr.length - 1);
        for (int i : arr) {
            System.out.println(i);
        }
    }

    public static void partial(int[] a, int left, int right) {
        if (left >= right) {
            return;
        }
        int key = a[left];
        int p_left = left;
        int p_right = right;
        boolean flag = true; // true移动右指针，false移动左指针
        while (true) {
            if (flag) {
                if (a[p_right] < key) {  // 基元素大于右指针所指元素，交换位置
                    a[p_left] = a[p_right];
                    flag = false;
                    p_left++;
                } else {
                    p_right--;
                }
            } else {
                if (a[p_left] > key) {  // 基元素小于左指针所指元素，交换位置
                    a[p_right] = a[p_left];
                    p_right--;
                    flag = true;
                } else {
                    p_left++;
                }
            }
            if (p_left == p_right) {  // 指针重合，基元素覆盖到指针处，跳出循环
                a[p_left] = key;
                break;
            }
        }
        partial(a, left, p_left - 1); //排列左子数组
        partial(a, p_right + 1, right); //排列右子数组
    }
}


[out]:
5
13
20
44
49
55
83
120
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def quick_sort(a, left, right):
    if left >= right:
        return
    p_left = left
    p_right = right
    key = a[left]  # 取区间第一个元素为基元素
    flag = True
    while 1:
        if flag:
            if a[p_right] < key:
                a[p_left] = a[p_right]
                p_left = + 1
                flag = False
            else:
                p_right -= 1
        else:
            if a[p_left] > key:
                a[p_right] = a[p_left]
                p_right -= 1
                flag = True
            else:
                p_left += 1
        if p_left == p_right:
            a[p_left] = key
            break
    quick_sort(a, left, p_left - 1)
    quick_sort(a, p_right + 1, right)


if __name__ == '__main__':
    arr = [34, 3, 65, 101, 11, 5, 23, 67, 344, 895, 56, 72, 45]
    quick_sort(arr, 0, len(arr) - 1)
    print(arr)
    

[out]:
[3, 5, 11, 23, 34, 45, 56, 65, 67, 72, 101, 344, 895]