二叉树基础

发表于 更新于 分类于 ，

前言

二叉树（Binary tree） 是一种基本的数据结构。许多问题可以抽象出二叉树的形式，其结构和算法均较为简单。主要用于提升搜索速度。

基本概念

节点

节点是二叉树中最基本的元素。在链表形式的二叉树中，一个节点包含的信息主要有此节点的值、子节点的指针（红黑树中还存在节点颜色信息等）。

image-20210407230430436
image-20210407230430436

节点的度

节点的度指的是此节点拥有子树的数量。在二叉树中，节点的度只能为0、1、2.

image-20210407230903553
image-20210407230903553

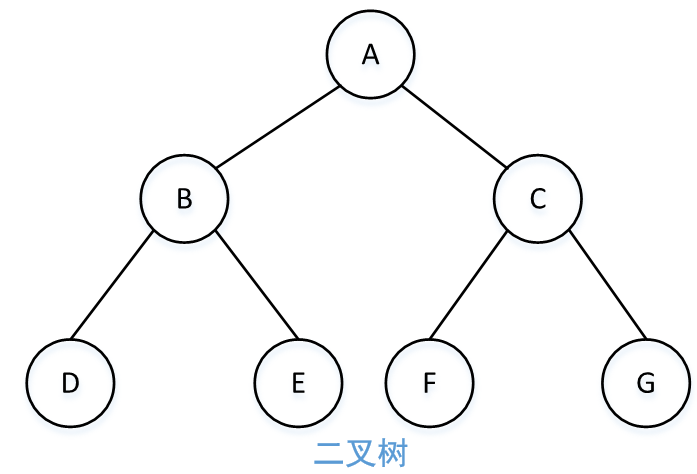
树

由节点组成的集合。

image-20210407231144714
image-20210407231144714

树的度

一个树的度为节点中度的最大值。

节点层次

树的每一行为一层，从根节点开始为第一层。

image-20210407231513569
image-20210407231513569

树的深度

树的深度即为节点的最大层次数。

二叉树的分类

斜树

所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

image-20210407232035962
image-20210407232035962

完全二叉树

树的每一层按从上到下，从左到右依次填充，中间不可有空（与数组的索引对应）。其特点为：

  1. 叶子结点只能出现在最下层和次下层；
  2. 最下层的叶子结点集中在树的左部；
  3. 倒数第二层若存在叶子结点，一定在右部连续位置；
  4. 如果结点度为1，则该结点只有左孩子，即没有右子树；
  5. 同样结点数目的二叉树，完全二叉树深度最小。
image-20210407232524762
image-20210407232524762

满二叉树

在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。 满二叉树的特点有：

  1. 叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
  2. 非叶子结点的度一定是2。
  3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。
image-20210407232725665
image-20210407232725665

扩充二叉树

扩充二叉树是对已有二叉树的扩充，扩充后的二叉树的节点都变为度数为2的分支节点。也就是说，如果原节点的度数为2，则不变，度数为1，则增加一个分支，度数为0的叶子节点则增加两个分支。

平衡二叉树

是一棵空树或它的任意节点的左右两个子树的高度差的绝对值不超过1

二叉树的存储方式

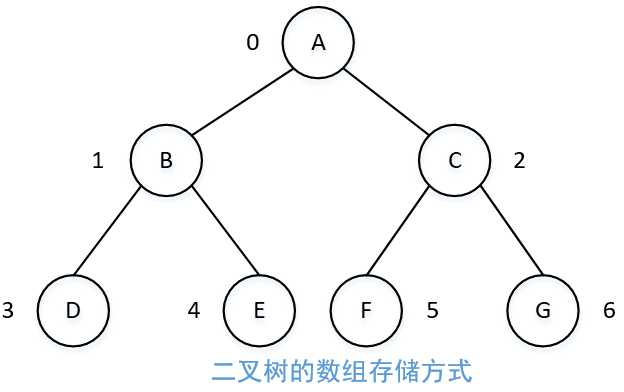
顺序存储

二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。这种方式适用于完全二叉树，应为完全二叉树的节点是按照顺序来分布的。当二叉树不为完全二叉树时，特别是当树为斜树时，会造成数组中许多索引处的值无效，浪费大量的空间。

image-20210407233505069
image-20210407233505069

链表存储

在结构体中直接定义两个孩子指针和一个数据储存区。

1
2
3
4
typedef struct BiTNode{
    TElemType data;//数据
    struct BiTNode *lchild, *rchild;//左右孩子指针
} BiTNode, *BiTree;

二叉树的遍历

二叉树的遍历方式主要有前序遍历、中序遍历、后续遍历三种。

前序遍历

从根节点出发，按照先左后右的方式遍历所有子树（父节点 - 左子树 - 右子树）。

1
2
3
4
5
6
7
8
void PreOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
    PreOrderTraverse(T->lchild);    /*再先序遍历左子树*/
    PreOrderTraverse(T->rchild);    /*最后先序遍历右子树*/
}

中序遍历

从最左子节点出发，按照左子树 - 父节点 - 右子树的顺序遍历。

1
2
3
4
5
6
7
8
void InOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    InOrderTraverse(T->lchild); /*中序遍历左子树*/
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
    InOrderTraverse(T->rchild); /*最后中序遍历右子树*/
}

后序遍历

从最左子节点出发，按照左子树 - 右子树 - 父节点的顺序遍历。

1
2
3
4
5
6
7
8
void PostOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    PostOrderTraverse(T->lchild);   /*先后序遍历左子树*/
    PostOrderTraverse(T->rchild);   /*再后续遍历右子树*/
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
}

二叉树的应用

普通的二叉树，很难构成现实的应用场景，但因其简单，常用于学习研究，平衡二叉树则是实际应用比较多的。常见于快速匹配、搜索等方面。
在二叉树建立的时候，通常按照左子树的数小于父节点、右子树的数大于父节点的规则来排序。这样在搜索的时候，可以将时间复杂度降低至\(O(logn)\)或者\(O(h)\) (\(h\)为树的深度)，大大提升搜索效率。